小学五年级数学问题提出能力与观念之间关系的研究,提高五年级小学生计算能力的研究

小学五年级数学问题提出能力与观念之间关系的研究

如何提高小学五年级学生计算能力的研究1。指导思想:新课程标准对小学数学计算指出，“学生应该能够正确地进行整数、小数和分数的四种计算。对于一些基本计算，它们应该达到一定的熟练程度，逐步达到合理灵活的计算方法”。小学数学教学贯穿于小学数学教学的全过程，即小学生的学习

五年级数学找 图形规律

新世纪(版)数学教材分析(五年级第一卷)新世纪(版)小学数学教材编写组本教材是根据《全日制义务教育数学课程标准(实验稿)》的基本概念和要求编写的，体现了新世纪(版)《义务教育课程标准实验教材数学》第二部分教材编写的指导思想和依据。现代教育观认为数学教学是数学活动的教学，即思维活动的教学。 如何在数学教学中培养学生的思维能力和良好的思维品质是教学改革的重要课题。 孔子说:“学而不思是无用的，思而不学是危险的。” 为了让学生在数学学习中积极思考，应该教学生分析和提问，给出问题，然后回答简单的加减乘除计算学习。五年级数学还涉及到小数、分数、三维图形等更难的内容，可以说是小学数学知识中更系统、更复杂的一部分。 然而，五年级的学生可能不可能第一次接受难学的数学知识，那么他们应该如何指导五年级的数学呢？其次，首先，这是一个孩子情绪和情感的突然时期——防止孩子形成叛逆的个性。孩子们通常在10岁左右，他们的自我意识开始提高。他们非常需要父母的尊重，他们需要父母像对待大孩子一样对待他们。 然而，许多父母不了解孩子的心理，仍然把孩子当孩子看待。因此，这个时期的孩子经常，

提高五年级小学生计算能力的研究

如何提高小学五年级学生计算能力的研究1。指导思想:新课程标准对小学数学计算指出，“学生应该能够正确地进行整数、小数和分数的四种计算。对于一些基本计算，它们应该达到一定的熟练程度，逐步达到合理灵活的计算方法”。小学数学教学贯穿于小学数学教学的全过程，即小学生的学习

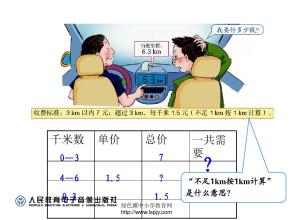
五年级数学找 图形规律

小学五年级数学问题提出能力与观念之间关系的研究范文

摘要：近几年来， 数学问题提出日益受到学者们的重视， 然而中国小学生数学问题提出能力与观念之间关系的研究不是很深入， 特别是数学问题提出能力的测量缺乏有效的评价指标。因此， 构建一个有效的数学问题提出能力的评价体系， 并在此基础上探究小学生数学问题提出能力和观念之间的关系就显得尤为重要。对辽宁省117名五年级小学生数学问题提出能力和观念的情况， 及其二者之间的关系进行调查。调查结果表明：首先， 大部分学生都能够提出正确的数学问题， 而提出创新性的， 复杂程度高的数学问题存在困难。同时， 学生对学好数学问题提出， 缺乏一定的信心。其次， 学生的数学问题提出能力和观念之间存在较高的相关性。
关键词：问题提出能力； 问题提出观念； 调查研究；

五年级学生数学问题提出能力与信念调查摘要:
在问题提出越来越受到研究者关注的同时，关于中国学生数学问题提出的信念与能力之间关系的研究，尤其是关于构建有效的问题提出评价体系的研究，至今仍被忽视。本研究旨在构建一个评价小学生数学问题提出倾向的方案，探讨中国小学生的问题提出能力及其与问题提出信念的关系。本研究对辽宁省117名五年级学生进行了问题提出能力测试。后来他们都收到了一份问卷。首先，问题提出能力测试的结果显示，学生能够提出适当的问题，但不能提出原始和复杂的问题。第二，问题提出问卷的结果显示，学生对做好问题提出缺乏信心。最后，我们发现学生的问题提出能力与信念之间有着密切的关系。
关键词:
问题提出能力；提出信仰的问题；调查研究；

1研究背景
近年来，数学问题的提出越来越受到学者们的关注。它被认为是数学课程的重要组成部分，甚至是[1~3]数学教学活动的中心。例如，中国2011年数学课程标准强调，在问题解决的课程目标中，学生应该“从数学的角度初步学习发现和提出问题”。综合运用数学知识解决简单的实际问题”[4]。2000年美国数学课程和评价标准[5]中也提到了数学问题的重要性。
鉴于数学问题在数学课程和教学中的重要作用，学者们对数学问题进行了一系列相关研究。例如，对数学问题提出能力水平的调查研究表明，中国中小学生提出数学问题的能力仍需提高[6~7]。摘要:通过对数学问题提出能力和数学问题解决能力之间关系的调查研究，揭示了学生数学问题提出能力和数学问题解决能力之间的高度相关性。[8~10]。学生数学问题提出能力评价研究认为，学生数学问题提出能力可以从流利性、灵活性和创新性三个方面进行评价，[11~21]。然而，从数学问题的流畅性、灵活性和创新性三个方面来评价学生提出数学问题的能力是不完整的。既然数学问题的复杂性也代表了学生提出数学问题的能力，那么学生提出的数学问题的复杂性也应该是他们提出数学问题能力的一个评价方面。同时，在提出数学问题的能力与提出数学问题的概念之间的关系的研究中，仍然存在一些空白度。学者菲利普和尼古拉对数学问题提出能力与概念[22]之间关系的研究提供了一些启示。他们调查了塞浦路斯五、六年级小学生数学问题提出能力和自我效能感之间的关系。结果表明，塞浦路斯小学生的数学问题提出能力与自我效能感有一定的相关性。然而，本研究仅考察了学生自我效能感概念与提出数学问题能力之间的关系，并未涉及学生的其他问题提出概念。例如，学生对提出数学问题的重要性的理解，他们对提出数学问题的兴趣，以及他们对提出数学问题的教学方法的理解。同时，能否有效测量提出数学问题的能力将直接影响研究者进一步探索提出数学问题的能力与概念之间的关系。因此，本研究将首先界定数学问题提出和数学问题提出的概念，并构建一套数学问题提出的评价体系。在此基础上，本研究调查了沈阳市小学生提出数学问题的能力和观念以及二者之间的关系。
2相关概念的定义
数学问题表述是指新数学问题的表述和对现有数学问题的重新解释，这些问题可能发生在数学问题解决之前、之中和之后[2]。学生在呈现数学问题的过程中会经历四个心理过程:理解信息、转换信息、编辑信息和选择信息[23]。对信息的理解发生在根据一些数学表达式提出数学问题的过程中。信息的转换发生在学生根据一些数学图片和表格提出数学问题的过程中。信息的编辑发生在学生根据一些数学信息和数学故事无限制地提出数学问题的过程中。信息的选择发生在学生根据一定的答案提出数学问题的过程中。思想是个人所持有的主观知识和理论，包括所有个人都认为正确但不能提供令人信服的证据的知识[24]。基于观念的概念，研究者认为数学问题提出的观念是指学生对提出数学问题的学习过程中的重要性、兴趣和信心的主观认识和态度。
3研究方法
3.1样本
调查了沈阳新民市69名五年级学生和朝阳北票市48名五年级学生提出数学问题的能力和观念。根据数学课程标准的要求，学生在考试前已经学习了因子与倍数、平行四边形、三角形面积、梯形面积、分数、分数加减等相关知识。此外，参与调查的学生对所提出的数学问题有一些了解，因为学生使用的数学教科书中有一些情况。
3.2测试过程
为了防止一些学生对数学问题仍不清楚，在测试前，研究人员解释了一个数学问题的例子:“在服装店，一件外套的价格是60元，一双鞋的价格是82元，数学问题是根据已知条件提出的。“如果学生在问数学问题时有困难，研究者可以举个例子:一件外套和一双鞋总共多少钱？然后根据情况引导学生提出其他数学问题。在解释了这些例子后，研究人员强调这个测试不是真正的测试，它的目的是了解他们提出数学问题的能力，所以在测试过程中不要紧张。在测试过程中，如果学生不理解问题的意思，老师可以给出必要的提示。数学问题提出测试结束后，将进行数学问题提出概念测试，这两个测试将花费大约50分钟。
3.3测试工具
数学问题提出能力测试包括六个数学问题提出测试问题[测试问题2限制学生用来提出数学问题解决策略的操作类型，以便检查学生在数学问题提出过程中理解信息的能力]。从提出问题的情况来看，有图片、答案、表达、语言描述和表格。例如，用1.6×8的计算方法(列)写两个应用问题。数学问题概念问卷包括20个五点李克特概念问题，涉及学生提出数学问题的重要性、学习过程中提出数学问题的信心以及提出数学问题的兴趣。就设计方法而言，这20个概念问题可分为10个正向问题和10个反向问题。例如，“虽然我努力学习，但我在问数学问题时总是遇到困难”是相反的问题。“我认为我可以从提出数学问题的过程中学到很多东西”是一个积极的问题。提问数学问题的能力和提问数学问题的概念问卷见附录1和2。
3.4评价标准
数学问题提出从流畅性、灵活性、新颖性和复杂性四个维度进行评价的测试。流畅性是指[评价一个数学问题是否是正确的数学问题的正确数学问题的数量，首先，评价所提出的数学问题是否满足课题的要求。其次，评估所提出的数学问题是否是可解的数学问题(不可解的数学问题意味着该数学问题的数学信息不足或与已知条件相矛盾)。最后，评估所提出的数学问题是否符合现实生活)。对于某个试题，如果学生问了一个正确的数学问题，他将得到1分，否则他将得到0分。灵活性(Flexibility)是指学生根据提出某个问题的情况，提出的两个数学问题类型的变化程度。如果两个数学问题都是错的，或者其中一个是错的，或者两个数学问题都是正确的并且属于同一类型，两个都得0分，如果两个数学问题都是正确的并且不属于同一类型，则得1分。数学问题的类型是根据数学问题的总语义类型来确定的。加减的语义类型分为三种:变化、组合和比较。乘法和除法的语义类型分为聚合、多重、矩形和等组组合[25]。例如，在测试1中，一个学生问了两个数学问题，“小明带了100元，买了两条围巾和一副手套，还剩多少？”“买两副手套和一条围巾要多少钱？”前一道数学题的语义类型发生变化，后一道数学题的语义类型被合并，学生试题1的灵活性维度得1分。新奇意味着学生提出的数学问题更具创新性。具体的评价方法是，如果某一类正确数学问题的数量少于所提出的所有正确数学问题数量的10%，那么这类数学问题就被评价为新的数学问题。在这个维度中，数学问题类型的划分方法与柔性维度的划分方法相同。如果学生提出一个新的数学问题，他或她将得到1分，而一个非新的数学问题或不正确的数学问题将得到0分。例如，在测试题5中，数学问题“第四天的正方形是第二天的正方形的多少倍？”一个被评价为新奇的数学问题得一分。复杂性是指学生提出的正确数学问题中包含的语义类型的数量。在某个试题中，如果学生提出的两个数学问题中至少有一个包含两种语义类型，则给出1分，如果至少有一个数学问题包含三种或三种以上语义类型，则给出2分，其余为0分(两个问题中至少有一个是错误的，或者两个数学问题都是正确的，但每个问题只包含一种语义结构)。例如，在测试问题6中，一个学生问了两个数学问题，“总共有多少只动物？”“草地上有5只母鸡和8头奶牛。草地上有几条腿？”第二个数学问题由两个语义结构组成:相等组的组合和聚集。学生试题6的复杂性维度得1分。数学问题提出能力测验的四个维度的分数反复累加，流畅性和创新性维度的总分各为12分，灵活性维度的总分为6分，复杂性维度的总分为10分，[测验项目2要求学生按照指定的公式写出数学问题，因此， 根据问题情境来评价学生提出的数学问题的复杂性是没有意义的]，所以数学问题提出能力测验的最低分是0分，最高分是40分。
在数学问题概念问卷中，逆向问题的得分是逆向的。例如，对于“虽然我努力学习，但我在问数学问题时总是遇到困难”的问题，“非常不同的意思”选项得5分，“不同意”选项得4分，“不知道”选项得3分，“同意”选项得2分，“非常同意”选项得1分。积极的问题得分积极。例如，对于“我能正确评估给定的数学问题是否正确”的问题，选项“非常不同的含义”得1分，“不同意”得2分，“不知道”得3分，“同意”得4分，“非常同意”得5分。数学问题概念问卷的最低分是20分，最高分是100分。
4研究结果

4.1数学问题提出能力的结果
从考试的整体情况来看，大多数学生都能提出正确的数学问题。数学问题提出能力测验四个维度的得分率分别为:流畅性:87.5%，灵活性:45.7%，创新性:12.3%，复杂性:20.3%。因此，在问题提出的流畅性维度上，学生的数学问题得分仍然相对较高。然而，也有一些学生问不符合要求的数学问题。例如，在试题2中，根据问题的要求，学生需要问应用问题，而有些学生问书面问题，如:“8 1.6的和是多少？”在试题4中，根据问题的要求，学生需要提出用乘法或除法(可以包括加法或减法)来解决的应用问题，而有些学生问:“小明省了250元，小李省了300元，小明比小李少得多？”在测试题5中，学生需要根据情境中隐含的规律提问，但是一些学生问，“第四天，他用23根火柴建造了多少个正方形？”显然，这个数学问题不符合问题中隐含的规律。在试题6中，一些学生问了一个数学问题:\"一只母鸡在一个有10个鸡蛋的世界里有多少个鸡蛋，那么五只母鸡在一个有30个鸡蛋的世界里有多少个鸡蛋？\"可以看出，提出的数学问题不符合现实生活。
与数学问题提出的流畅性维度相比，学生在数学问题提出能力的创新性维度和复杂性维度上的表现不容乐观。学生们倾向于问一些简单的数学问题，类似于教科书，并且在实践中很常见。例如，对于试题1，它类似于“买两双鞋和一副手套要多少钱？”合并的问题是36%。它类似于“两双手套多少钱？”等效群体聚集问题为26%。
4.2提出数学问题想法的结果
从数学问题概念问卷来看，一些学生对数学问题的想法并不乐观。例如，38%的学生在概念问题4“虽然我努力学习，但我问数学问题时总是遇到困难”，同意或非常同意，这表明很大一部分学生对学好数学问题缺乏一定的信心。至于问题19，“我愿意问类似教科书中的数学问题”，高达62%的学生选择同意或非常同意，这可能是学生数学问题创新性较低的原因之一。然而，学生们非常喜欢数学问题引发的活动。例如，关于概念问题15，“如果数学课能给学生提供更多的数学问题提出活动，数学课就会变得更有趣，”90%的学生选择同意或非常同意。
4.3数学问题提出能力与概念的关系
皮尔逊相关分析表明，首先，学生的数学问题提出能力与概念在0.05的显著水平上呈正相关(ρ=0.21，P = 0.02)；学生提出数学问题能力的创造性与显著性水平0.05正相关(ρ=0.27，P=0.00)。其次，数学问题提出的四个评价维度的创造性和灵活性(ρ=0.29，P=0.00)和复杂性(ρ=0.40)。P=0.00)在0.05[的显著性水平上是正相关的，只有数学问题提出的灵活性，复杂性和创新性之间的相关性在研究中被计算出来，正确性不包括在内，因为灵活性、复杂性和创新性三个维度都是以正确性为基础的，也就是说，只有正确的数学问题才能评价它们的灵活性、复杂性和创新性]。最后，学生的数学问题提出概念可以很大程度上预测他们的数学问题提出能力(r = 0.21，f = 5.47，p = 0.02)。
5讨论
通过这项研究，可以得出结论，学生倾向于提出一些常规的和熟悉的数学问题，而不是创新的和复杂的数学问题。因此，在日常教学活动中，教师需要把培养提问能力作为一个重要的教学目标，并在每个学习环节的课堂教学中实施。
首先，教师不仅要提供丰富多彩的数学情境，激发学生提问数学问题的欲望，鼓励学生提问数学问题，还要教会学生一些提问数学问题的方法，并在提问数学问题的过程中给予一些帮助。例如，当学生不能问数学问题时，给他们举一些例子，当学生总是从其他角度问类似的数学问题时，给他们举一些例子，鼓励学生评价和思考提出的数学问题。此外，仅仅依靠课堂教学来促进学生数学提问能力的提高是不够的。还有必要依靠各种考试对数学教学的影响，即在考试中加入一些数学问题中的试题。当然，还需要进一步研究在考试中加入什么形式的数学问题。
其次，由于提出数学问题的概念与学生提出数学问题的能力有着密切的关系，我们应该重视培养学生提出数学问题的概念，让学生认识到提出数学问题与解决数学问题同等重要。提出一个好的数学问题也是智力的重要表现。与此同时，学生应该得到更多的鼓励，并且对学好数学问题有信心。
第三，数学问题提出能力的培养应从低年级开始。调查的样本是五年级学生。研究发现，一些学生已经初步形成了只解决数学问题而不适应提出数学问题的习惯，这将抑制学生创造力的发展。然而，低年级学生还没有形成固定的学习习惯和思维习惯，这是高度可塑性的。因此，抓住机会提高低年级学生的数学意识和能力是非常重要的。
最后，应该指出，这项研究有某些局限性。首先，数学问题提出的试题选自算术领域，而不是几何和概率统计领域。此外，提出的数学问题的类型仅限于问题解决之前提出的数学问题，而与问题解决期间和之后提出的数学问题无关。因此，使用问卷提问数学问题的能力不能代表学生提问数学问题的综合能力。其次，数学问题提出的评价标准需要进一步完善。例如，数学问题类型的分类标准是否合适，创新数学问题的比例(10%)是否合适，需要进一步验证。
参考
[1]布朗斯一世，沃尔特m i. 1993。
[2]银易安.关于提出[的数学问题.数学学习，1994，14 (1): 19-28。
[3]英语1d五年级儿童问题的发展——提出能力[j]。数学教育研究，1997，(34): 183-217。
[4]中华人民共和国教育部。数学课程标准(2011版)[硕士。北京:北京师范大学出版社，2011。
[5]全国数学教师理事会。学校数学的原则和标准[。弗吉尼亚州莱斯顿:作者，2000年。
[6]曾晓萍、卢传涵、王冰夷。初中生“问数学问题”的现状及对策[。数学教育杂志，2006，15 (3) :51-53。
[7]英语法学博士。正式和非正式语境中的儿童问题提出[。数学教育研究杂志，1998，29 (1) :83-106。
[8]蔡杰，银英.解决剩余故事除法问题的解决过程和解决方案的解释:中美学生有相似的困难吗？[.数学教育研究杂志，1995，(26): 491-497。
[9]陈丽敏、列文·韦尔沙费尔、李薛梅。提出问题与解决问题之间关系的问卷调查[。数学教育杂志，2004，13 (4): 70-74。[/BR/] [10]陈升，范东文，陈问，等.中国小学生提出和解决算术应用题的关系.[9]韩国数学教育学会学报系列D:数学教育研究，2007，11 (1): 1-31 .
[11]夏晓刚、王冰夷、卢传涵。对中小学生数学提问能力评价的再探索[。数学教育杂志，2008，17 (2) :8-11。
[12]蒋志平。知识要素研究与问题的主动设计[。数学教育杂志，2011，20 (2) :69。
[13]王策。创造数学问题情境应注意的几个关系[。数学教育杂志，2009，18 (3) :31。
[14]王存荣。在反思性数学教学中培养学生提问的能力[。数学教育杂志，2009，18 (1) :45。
[15]张于霞，俞平。基于关系表示复杂性模型的问题图式分层研究[[]。数学教育杂志，2009，18 (4) :46。
[16]王志明，马福。《小学数学教师教学问题意识调查》，[。数学教育杂志，2009，18 (6) :34。
[17]曾晓萍、王冰夷、卢传涵。对数学“情境-问题”教学中数学探究学习的思考[。数学教育杂志，2009，18 (1) :82。
[18]王维彪、张淼、余如玉。《初中数学“情境-问题”教学的校本研究》，[。数学教育杂志，2009，18 (1) :88。
[19]鲍建利。初中数学“情境问题”教学的校本研究——以[《握手问题》教学为例。数学教育杂志，2009，18 (1) :93。
[20]王维彪。初中数学“情境-问题”教学的校本研究——以“图形面积等分”[为例。数学教育杂志，2009，18 (1) :96。
[21]郑建远。初中数学“情境-问题”教学的校本研究——以“用等边长正多边形铺地板”为例的教学案例[。数学教育杂志，2009，18 (1): 99。
[22]菲利普·g，尼古拉·a .有效信念、问题提出和数学成就[·R]。欧洲数学教育研究学会第五届大会记录。塞浦路斯，拉纳卡，2007年。
[23]克里斯托·C，穆苏利德斯·N，皮塔利斯·M，等.问题提出过程的经验分类法[]。ZDM:数学教育国际评论，2005，(37) :149-158。
[24]佩科宁E .数学课堂中的一个隐性调节因素:数学相关信念[A]。作者:阿蒂·姆，比约克奎斯特·奥，佩科宁·埃，等。数学与科学教育研究[。教育研究所。Jyvaskyla大学，2001年。
[25]魏尔夏费尔，德·科特E .数字和算术[A]。作者:毕晓普、克莱门茨·金、凯特尔·C等。[国际数学教育手册。多德雷赫特:克鲁沃，1996年。